Brief on Information Theory

Information Theory, according to Wikipedia, delves into the quantification, storage, and communication of information. But what does “information” truly signify?

What is Information?

One way to understand information is through the concept of surprise related to an event (X=x) . The surprise associated with an event is inversely related to its probability; the higher the probability, the less surprising the event. This relationship can be expressed as

$$I(X=x) = \frac{1}{p(X=x)}$$

This would look as follows

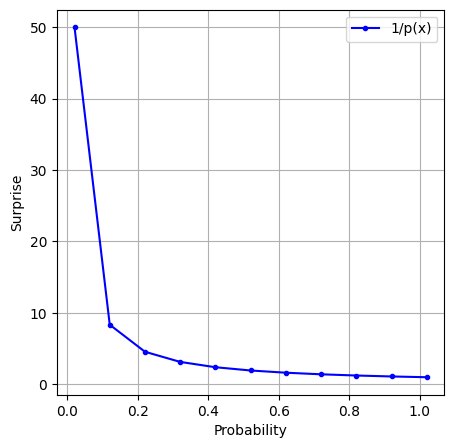
In this formulation, the surprise associated with a probability of 1 is 1, and it increases as the probability decreases. However, we aim for zero surprise when an event is certain (probability of 1). To achieve this, we refine the definition using the logarithm function, as the logarithm of 1 is 0. This yields a new definition of information:

$$I(X=x) = \log\left(\frac{1}{p(X=x)}\right) = - \log\left(p(X=x)\right)$$

Here’s the comparitive view of this with previous defination.

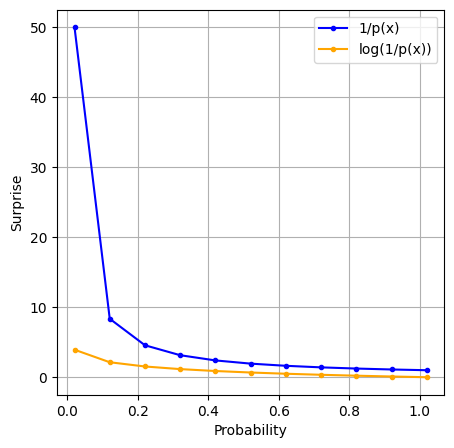
We observe that the surprise goes to 0 as the probability approaches 1.

Understanding Entropy

So far, we have understood the notion of surprise corresponding to an outcome of an event. What would be this surprise corresponding to a distribution? This is referred as Entropy. It is the expectation over the measure of information or surprise in the outcome of a random variable. The more uncertain or surprising the outcomes, the higher the entropy. It’s expressed as follows:

$$H(X) = -\sum_{k=1}^{K} \left(p(X=k) \log \left(p(X=k)\right) \right)$$

Do note:

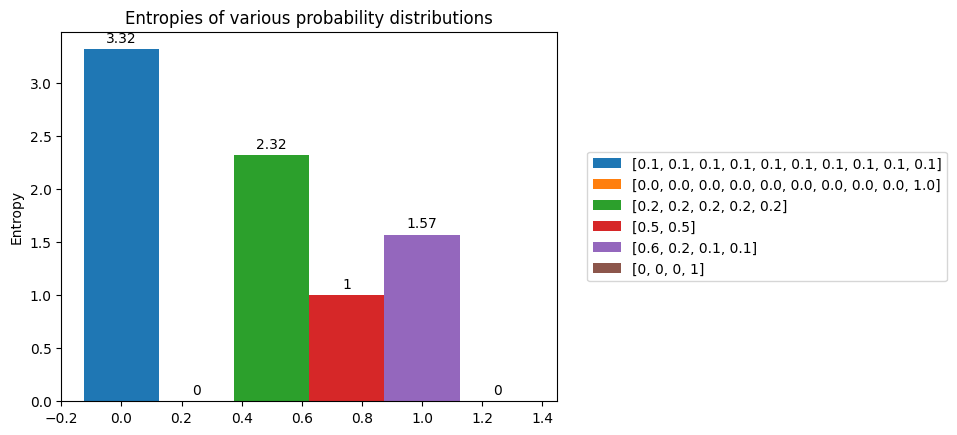
• A uniform discrete distribution has the highest entropy. For a uniform categorical distribution with K labels, the entropy would be log(K)
• A deterministic distribution has the least entropy.

Now, let’s visualize entropy for different probablity distributions.

<matplotlib.legend.Legend at 0x1097d3b10>

Joint Entropy

It’s the entropy corresponding to join distribution of two random variables i.e.

$H(X,Y) = \mathop{\mathbb{E}}[I(X,Y)]$

$H(X,Y) = - \sum_{x \in X} \sum_{y \in Y} p(X=x, Y=y) \log(p(X=x, Y=y))$

Conditional Entropy

It’s the entropy corresponding to conditional distribution of random variable X given Y i.e.

$H(X|Y) = \mathop{\mathbb{E}}[I(X|Y)]$

$H(X|Y) = - \sum_{x \in X} \sum_{y \in Y} p(X=x, Y=y) \log(p(X=x|Y=y))$

Do note that the sampling of events is still done under joint distribution.

Chain Rule

It suggests: $$H(X,Y,Z) = H(X) + H(Y|X) + H(Z| X,Y) $$

Relative Entropy/ Kullback–Leibler (KL) divergence

The Kullback–Leibler distance, represented as $D(P\parallel Q)$, quantifies the expected difference in surprise between a source distribution (Q) and a target distribution (P), or how one distribution diverges from another. This can be understood as follows:

$D(P \parallel Q) = \mathop{\mathbb{E}}_{x \in X} \left[-\log(q(X=x)) - (-\log(p(X=x))) \right]$

$D(P \parallel Q) = \mathop{\mathbb{E}}_{x \in X} \left[-\log(q(X=x)) + \log(p(X=x))) \right]$

$D(P \parallel Q) = \mathbb{E}_{x \in X} \left[ \log \left( \frac{p(X=x)}{q(X=x)} \right) \right]$

$D(P \parallel Q) = \sum_{x \in X} \left[ p(X=x) \log \left( \frac{p(X=x)}{q(X=x)} \right) \right]$

Note:

• Sampling of events happens under the true distribution P.
• It’s non-symmetric (thereby not a true measure of distance) i.e. $D(P \parallel Q) \neq D(Q \parallel P)$
• $D(P\parallel Q)=0$ when $P=Q$

Mutual Information

It’s the relative entropy between true joint probability distribution (P(X,Y)) and the product distribution P(X).P(Y)

$ I(X;Y) = D(P(X,Y)\parallel P(X).P(Y))$

$ I(X;Y) = \sum_{x \in X} \sum_{y \in Y} p(X=x,Y=Y) \log\left(\frac{p(X,Y)}{P(X).P(Y)}\right)$

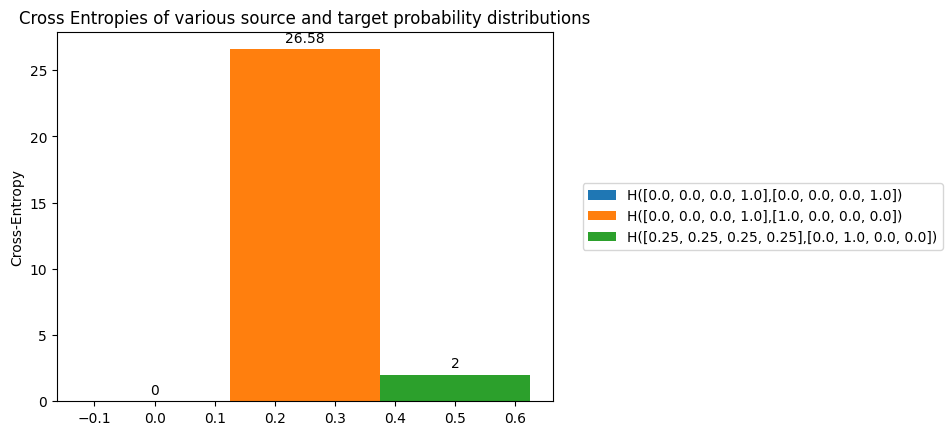
Cross Entropy

Let’s say that we have a assumed probability distribution $(Q)$ of observing events $X$. However, let’s assume the true probability distribution of observing $X$ is $P$. Estimating entropy of distribution Q when events happen under P is referred as Cross-Entropy.

$$H(p,q) = -\sum_{k=1}^{K} \left(p(X=k) \log\left(q(X=k)\right)\right)$$

This entropy would be high only when unlikely events under P are considered to be highly likely under Q and vice-versa.

<matplotlib.legend.Legend at 0x10981cc90>

Cross Entropy and Relative Entropy ( KL)

$H_{cross}(P,Q) = H(P) + D(P \parallel Q)$

Let’s understand it by deriving it:

$ H(P,Q) = - \sum_{x \in X} P(X=x) \log\left(Q(X=x)\right)$

$ H(P,Q) = - \sum_{x \in X} P(X=x) \log\left(Q(X=x). \frac{P(X=x)}{P(X=x)} \right)$

$ H(P,Q) = - \sum_{x \in X} P(X=x)\log\left(P\left(X=x\right)\right) + \sum_{x \in X} P(X=x) \log\left(\frac{Q(X=x)}{P(X=x)}\right)$

$ H(P,Q) = H(P) + D(P \parallel Q)$

This also means that minimizing “Cross entropy” is same as minimizing “KL” as “$H(P)$” is not controlled.